Como controlar a produção e o estoque de uma indústria
Atualizado em 22/04/25 - Escrito por Thiago Leão na(s) categoria(s): Produção
Controlar a produção e o estoque são processos realizados por indústrias para garantir que os produtos fabricados atendem as especificações planejadas pela equipe da empresa e pelos clientes da fábrica. Também servem para evitar perdas e desperdícios, aumentando a competitividade e a lucratividade da empresa.
Esse aspecto da gestão industrial muitas vezes acaba sendo negligenciado por pequenas e médias indústrias, que realizam o controle da produção de forma ineficiente, utilizando planilhas, documentos de papel ou até sem qualquer tipo de controle.
Nesse artigo irei cobrir quais são os principais pontos que a sua indústria precisa se preocupar para aplicar um bom controle da produção e o estoque. Confira:
Índice do artigo
Planeje e Controle sua Produção (PCP)
PCP é o processo ideal para gerir a sua produção e o seu estoque. Através dele, você garante que sua fábrica está produzindo os melhores produtos, dentro das melhores condições e conforme o planejado. Sem planos e controles, uma indústria terá dificuldade em se manter competitiva e oferecer qualidade.
O PCP, para ser mais concreto, serve para que a indústria atinja 4 objetivos:
- Programação da produção;
- Carregamento de máquinas e postos de trabalho;
- Sequenciamento e priorização da produção;
- Monitoramento da produção.
Engenharia do produto – Lista de materiais
O primeiro passo para controlar a produção de uma indústria é criar uma estrutura para o seu produto. Ou seja, criar uma engenharia para ele, onde você entenda bem como é composto o seu produto.
Caso a sua indústria ainda não possua uma estrutura bem definida dos produtos fabricados, esse é um alerta vermelho. A sua empresa precisa conhecer muito bem os produtos que fabrica e negocia para evitar perdas e prejuízos.
Essa estrutura é conhecida por alguns nomes, como engenharia do produto, lista de materiais ou BOM – bill of materials.
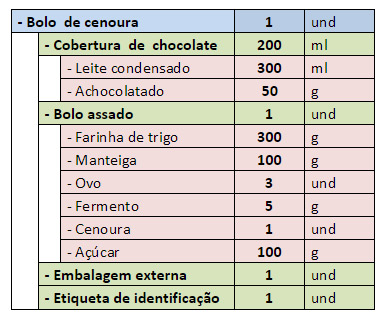
Para configurar uma lista de materiais é preciso seguir alguns passos básicos, sendo eles:
- Identificar todas as matérias-primas
- Identificar todos os produtos intermediários
- Identificar todos os produtos acabados
- Checar duplicidades
- Identificar os níveis da estrutura
- Cadastrar listas de materiais dos produtos intermediários
- Cadastrar a lista de materiais dos produtos acabados
Alguns pontos que não devem ser considerados na hora de montar sua lista de materiais:
- Itens de custo da máquina
- Itens compartilhados
- Itens raramente utilizados ou de valor insignificante
Exemplo de lista de materiais no sistema Nomus ERP Industrial:
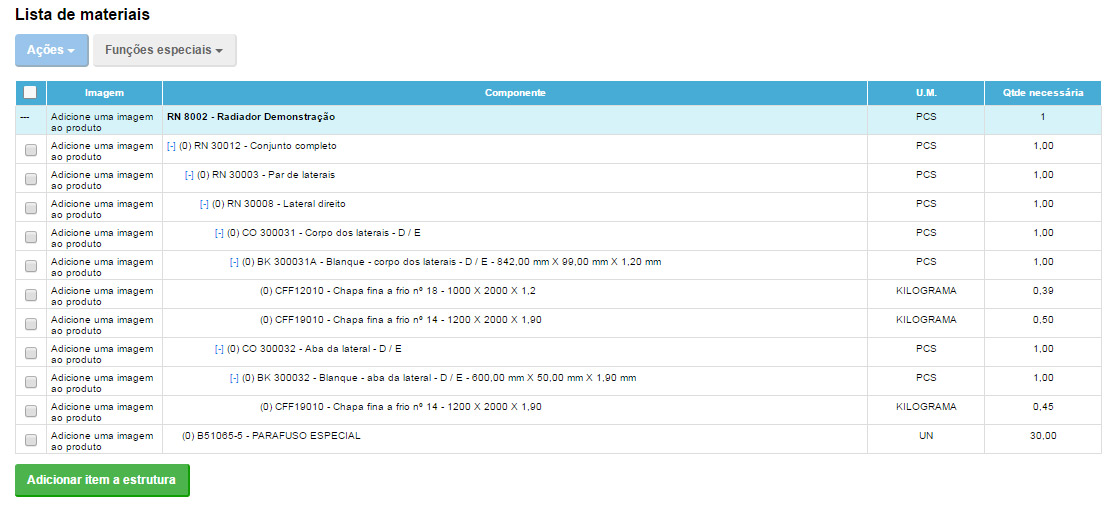
Aprenda mais sobre como montar a sua lista, recomendo que baixe o ebook:
Ordem de produção
O segundo ponto é iniciar a sua produção. Existem algumas formas de se fazer isso, como a produção empurrada e a produção puxada, sendo uma para estoque e outra sob encomenda.
Pegando como exemplo a produção puxada, a produção se inicia no setor de vendas, que ao vender um produto, abre uma ordem de produção para o mesmo.
Em uma indústria sem organização a produção pode começar por achismo de um líder de produção, ou ainda alguém gritando na fábrica: “Produz aí 50 bolos de cenoura”.
Esse tipo de gestão pode acarretar em diversos prejuízos para fábrica e por isso é fundamental que a empresa implemente um sistema de ordens de produção, onde o setor de PCP consiga comandar a cadencia da produção da fábrica.
Essa ordem de produção contém as informações necessárias para a produção dos produtos. Sendo as principais informações:
- O item que vai ser produzido, com seu código e descrição
- A quantidade que vai ser produzida
- A data de entrega planejada
Caso algum material esteja faltando no estoque, é possível abrir uma solicitação de compra automaticamente.

Veja também: Como criar uma indústria do zero com 8 passos
Veja também: Planilha de controle de estoque eficiente [GRÁTIS]
Gestão de compras
Para controlar a produção e o estoque de forma eficaz, é fundamental que a empresa possua algum tipo de geração de solicitações de compra para montar uma boa gestão de compras. O ideal é que seja feita de forma automatizada com o sistema de gestão, onde o programa identifica que falta algum material e assim gera uma solicitação de compra para ele.
Com a solicitação feita, a sua equipe pode fazer uma solicitação de cotação, caso desejar pesquisar o melhor preço entre os fornecedores disponíveis, ou gerar um pedido de compra diretamente com o fornecedor padrão.
Em um sistema de gestão ERP seria possível gerar as contas a pagar de forma automática integrada ao pedido de compra.
Requisição de materiais
O próximo passo para controlar a produção e o estoque de forma básica é possuir alguma forma de requisitar materiais empenhados. Ou seja, quando sua equipe for produzir o produto, ela precisa requisitar os materiais certos na quantidade correta ao estoque de matéria-prima.
Com um sistema ERP é possível fazer isso de forma integrada ao estoque e a lista de materiais do produto. Sendo assim, evita erros humanos e possíveis falhas de planilhas com dados errados ou desatualizados.
Reporte da produção
Por fim, pode parecer trivial mas boa parte das indústrias acabam não registrando quanto produziram e assim não sabem qual seu rendimento, perdas etc. O reporte da produção é uma cultura fundamental para qualquer indústria que deseja controlar a produção e o estoque de forma eficiente.
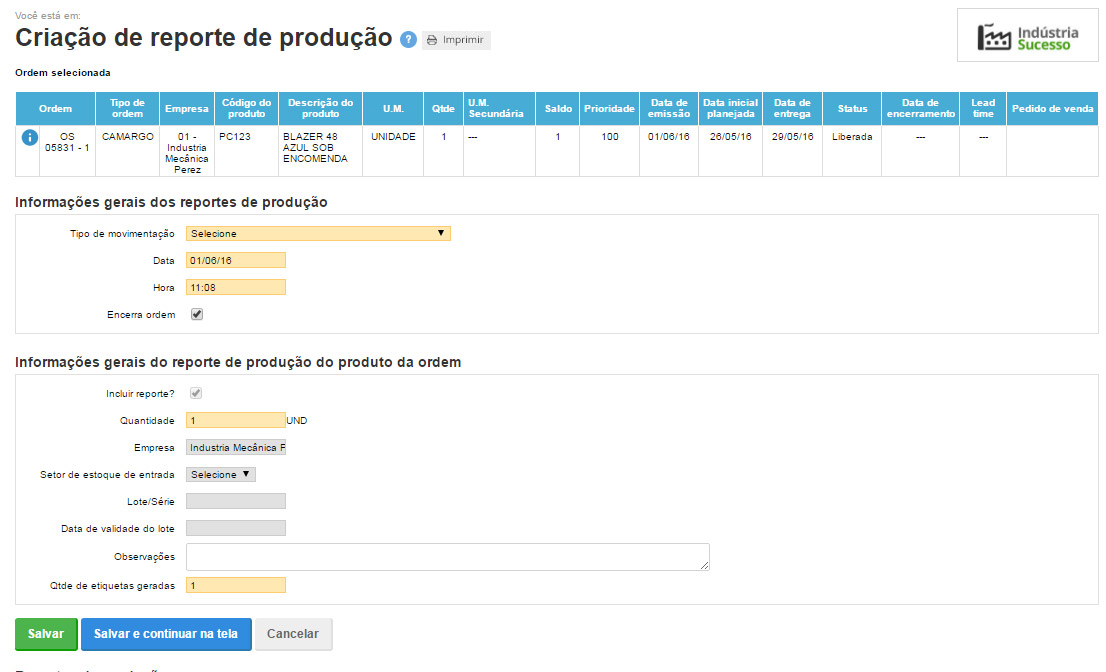
Principais benefícios de controlar a produção e o estoque de uma indústria
Ao realizar as etapas anteriores a sua indústria fica muito mais organizada e eficiente, já que consegue controlar melhor a produção e o estoque de maneira geral. Isso gera diversos benefícios para empresa, como por exemplo:
- Integração entre as áreas da empresa, gerando uma gestão integrada entre vendas, produção, estoque, compras e financeiro;
- Estoque atualizado, já que o sistema manterá o estoque sempre alinhado com a produção e a realidade da empresa;
- Custo da produção mais apurado;
- Rastreabilidade dos materiais.
Coloque em prática na sua fábrica
Controlar a produção e o estoque de uma pequena ou média indústria pode ser mais fácil do que você imagina e os benefícios são muito valiosos.
Recomendo que você assista uma demonstração do Nomus ERP Industrial e veja na prática como a ferramenta pode auxiliar a sua equipe a colocar esses controles em prática.
A Nomus oferece planos especiais para indústrias no simples nacional, além de um pacote de treinamento gravado completo e uma consultoria em gestão industrial.
Fique a vontade caso tenha alguma dúvida ou sugestão. Até a próxima!
Autor do Artigo
Thiago Leão
Engenheiro Mecânico Industrial formado na UERJ, Sócio e diretor comercial da Nomus. Thiago já atuou em fábricas de diversos setores, como: Embarcações, perfuração submarina, metal mecânica, materiais de escritório, alimentício, cosméticos e tubulação.
Encontre Thiago Leão nas redes sociais:
Um comentário
Participe! Deixe o seu comentário agora mesmo:









Agradeço Nomus material didático de grande relevância para a gente , média e pequena empresa Indústria